I am especially pleased to be included in this seminar, because I think that the subject we will be discussing is an important one. Also, I recognize that I am in the company of a very distinguished and technically sophisticated group, and I expect to learn a great deal from all of you before the day is over.

My own purpose is to discuss some of the philosophical ideas that underlie the practice of risk assessment. As a mathematician I may tend toward the abstract, and I hope that what I have to say is nevertheless relevant. Specifically, I intend to say a few words about the scope and origins of risk analysis, about the techniques analysts use, and the obstacles they must overcome. In the end I will try to identify three distinct situations in which risk analysis can be applied, and touch upon the different demands that each of these situations places on the analyst.

I will begin with some definitions. Risk is the possibility of loss from events with low probabilities but severe consequences. Risk analysis refers to the processes we use to evaluate those probabilities and consequences, and also to the study of how we incorporate the resulting estimates into our decision-making processes.

In some ways, the risks of a proposed activity are just another component in the total costs of that activity. Most costs involve some degree of uncertainty, and in making decisions about the activity, the costs need to be balanced against equally-uncertain benefits. In some ways, however, risks are very different from other costs, and for several reasons they require separate theoretical treatment.

First, there are both theoretical and practical difficulties involved in estimating the probabilities and consequences of low-probability events. These difficulties often lead to disagreements, even among experts; and these disagreements lead in turn to the low credibility that risk assessments sometimes suffer in public controversies.

Second, there will always be value questions which come into play, as when human lives must be balanced against economic considerations, or when the large amounts of money involved make expected monetary values a poor measure of a decision maker's utility.

And finally, risks are sometimes borne involuntarily by persons who are not otherwise involved in the activity. This is the case, for example, of fishermen or coastal residents who have no particular interest in offshore drilling, but who would be injured by environmental damage from serious oil spills.

Attention to these issues has contributed to the rise of the modern discipline of risk analysis. Actually risk analysis represents a merging of two distinct sub-disciplines, with common concerns but different roots. One requires the work of specialists, the other that of generalists.

The first of these sub-disciplines has its roots in the engineering professions. The modern techniques of this sub-discipline may be traced back at least to the beginnings of the U. S. space program, and have been developed most vigorously in the nuclear power industry. In the nuclear power industry these techniques are collected under the rubric of Probabilistic Risk Assessment (PRA), and they are sufficiently mature as to be on the route to standardization. PRA already has a formal place in some regulatory systems.

Independent developments have taken place in the design of other vehicles and other energy facilities, in environmental studies, and in safety studies of drugs and food additives. There has been a parallel development in military operations research, in which the subject matter is different but the challenges are the same; i.e., lack of data to support objective probability estimates, persistent value questions, and conflicting interests in complex decision processes.

In all of these areas the major issue is risk assessment; that is, identifying in detail the specific hazards of a given technology, and evaluating the probabilities and consequences of these hazards. These questions tend to be the domain of specialists, since they require intimate knowledge of the technologies involved.

The second sub-discipline cuts across all of these technologies, and is therefore the domain of generalists. This tradition has its roots in economics and operations research, and more particularly in the subject of decision analysis as taught by Howard Raiffa and others.

Keeney and Raiffa (reference [a]) characterize the two facets of risk analysis as the "uncertainty side" and the "value side." The uncertainty side deals with estimation of probabilities and consequences, and the value side deals with the requirements of rational decision making once these estimates are available. On the uncertainty side, we try to quantify the risks; and on the value side, we try to identify what level of risk constitutes an "acceptable risk."

Another element of this second sub-discipline involves attention to the sociological aspects of risk analysis. Studies have been made of the processes by which communities and societies make decisions involving risky technologies. These studies, of which reference [b] is a leading example, have helped to shed light on the risk analyst's role in the political process. Reference [c] is a good general source for this aspect of risk analysis.

Also addressed by the generalists are questions about the theoretical limits of risk assessment and its methods. Alvin Weinberg has used the term "Transscience" to refer to events of the type we are concerned with (reference [f]). Science is the study of repeatable phenomena, and these low-probability events are by definition not repeatable within our limited experience. Estimation of their probabilities is therefore, in one sense, beyond science, and although the questions are questions of fact, science cannot provide absolute answers. I do not know to what extent this characterization is sound in a philosophical sense, but it is certainly true in a practical sense, when experts lack the data or methods to make non-controversial predictions.

Since I intend to make frequent use of the words "objective" and "subjective," I will take a moment to say what I mean by them. By an objective determination of a probability or consequence, I mean an estimate sufficiently based on reliable data or logic that all responsible scientists can be expected to agree on it, or at least to settle their disagreements by the scientific methods of their professions.

In other circumstances, an evaluation is called subjective. An analyst might prefer to avoid stating a conclusion in such cases, but a decision maker has no such luxury. He must act; and if he is to act rationally his actions must reflect some consistent set of assumptions, even if the assumptions involve intuition and guesswork. These assumptions include his subjective probabilities. He may make use of expert advice, but ultimately he must decide for himself where to place his bets.

I will now briefly review some of the techniques analysts use to estimate the probabilities of low-probability events. All of these methods share one common feature: there is some degree of subjectivity in their inputs, and hence, in their final answers.

1. Statistical inference is the method of choice when there is a completely adequate data base. I mean here nothing more complicated than frequency counts based on a historical or experimental record. In risk analysis, however, the data base is inevitably too small, and must therefore be expanded by considering cases which are not strictly comparable to the case at hand. The subjectivity then lies in the extrapolation from historical or laboratory conditions to the conditions of the real world. The Commission will appreciate the difficulties involved if it has tried, for example, to make use of the accumulated experience of drilling rigs in the Gulf of Mexico to support predictions about what will happen in the Labrador Sea.

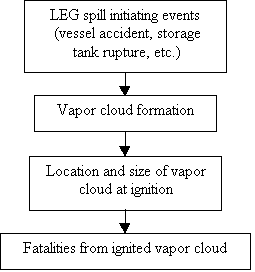
2. Construction of scenarios is a means of dividing an intractably large problem into smaller parts. Figure 1 is an example. This is from Ralph Keeney's analysis of the risk of a large-scale explosion at the proposed site of a liquid-natural-gas terminal in California (reference [e]). I present it here only to illustrate the degree of detail involved, which is not very great. The scenario describes an accident from the initial tank rupture through the final count of casualties in a simple four-part diagram. Each part requires its own sub-analysis. Each of the sub-analyses remains "transscientific," but perhaps less so than the original problem. Each part of the diagram lies within the expertise of a separate group of experts. Introduction of a scenario such as this one into a scientific debate can help the participants to identify their areas of agreement, and the areas in which further research might produce agreement.

In most problems, one would need to analyze more than one possible accident scenario.

3. Fault trees and event trees are an elaboration on the scenario method. Figure 2 is an extremely simple example of a fault tree, from a 1970 paper by John Garrick (reference [d]). A fault tree describes a system, such as a nuclear power plant or a drilling unit; and each node represents a component or subsystem whose failure rate can be determined from experience. The example describes a system with three components x₁, x₂, and x₃, such that the system fails if x₁ fails and either x₂ or x₃ also fails. Several equivalent representations are given. If we make a leap of faith and assume the component failure rates to be independent, then we can compute the probability of system failure. The calculation is carried out approximately in the figure. There are computer programs to do the same calculation for larger fault trees.

Of course subjectivity is not eliminated, even if the component probabilities are completely objective. The subjectivity lies in the structure of the tree itself, and in the ways in which the probabilities are combined. We have, therefore, a paradox: the larger and more detailed the fault tree, the less objective are the final results.

I want to dwell for a little while on the issue of combining probabilities, with or without

statistical independence. In Figure 2, it is assumed that the failure probability for each of the three components is .01. By assuming that these probabilities are independent, we can conclude that the probability that the entire system will fail is about .0002. But now suppose that the components, while independent in the sense of physical separation, are related in that they all tend to fail under similar conditions. For example, support that they all fail by overheating when the system is operated for too many hours on a hot day. Then the component probabilities are not independent. In the worst case, if the fatal conditions arise with probability .01 and cause all of the component failures, then the three component failure rates are completely correlated. In this case the system will fail with probability .01, an answer which differs by a factor of fifty from the answer we calculated in the "independent" case.

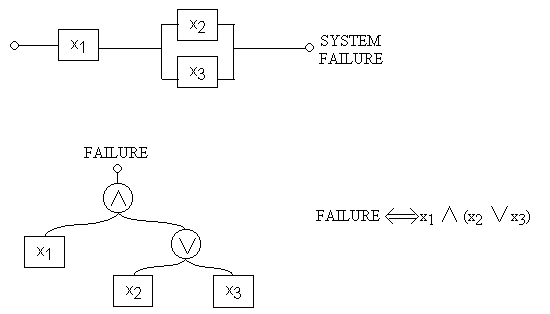
Evaluation of system failure probability in "independent" case:
If P(x₁) = P(x₂) = P(x₃) = .01, then                                  
            P(System Failure) » P(x₁) ( P(x₂) + P(x₃) ) = .0002

It is my feeling that in most cases, the assumption of independence of component probabilities flies in the face of common sense, and yet I know of no other basis for combining the probabilities which is not essentially subjective.

There are other graphical methods for risk assessment, mostly equivalent in principle to fault tree analysis. Terms for these methods have sometimes acquired specific meanings as terms of art within particular industries. For example, in the nuclear power industry, fault trees are used to compute system failure probabilities, while event trees are used to estimate consequences of failures.

4. Construction of system models is a further elaboration. A model can be simple or complex; it may be based on a few scenarios or a detailed fault tree. Typically models are very complex, and involve detailed computer simulations, often using Monte-Carlo techniques. The big disadvantage of these simulation models is that the complexity of the computer programs tends to obscure the underlying assumptions and inevitable subjective inputs. If a large-scale model is rushed into service, the overall complexity may serve to mask some very simplistic modeling at the lowest level.

However, system models also offer one major advantage: they can make other predictions in addition to accident rates, and these predictions can often be validated by experience. For example, a model might predict whether a drilling platform would capsize in a storm, a prediction we would not want to test by experience. But the same model might also predict how far the platform would roll in ordinary wave action, and a test of the latter prediction might justify confidence in the model even if its subjective inputs remained obscure or in doubt.

System models are the stock in trade of military operations research, where of course they are used for much more than evaluation of low-probability events. Construction of a system model is a major undertaking and the quality does not always warrant the investment. Still, a well-designed and tested model may be of enormous value to a decision maker.

I can think of three situations in which the methods of risk analysis can be usefully applied. They are, first, as an adjunct to the design process; second, as an input to a decision by a single decision maker; and third, as an element of a complex, multi-party decision process. All three types of application are potentially relevant to the issues before the Commission, but they are very different in the demands they place on the analyst.

They are so different, in fact, that the content of a proper risk analysis in one of the applications may bear little resemblance to the content of a proper risk analysis in either of the other applications. I make this point because I appreciate, for example, the essential role of detailed fault trees in design work, but I question their usefulness in demonstrating the overall safety of a system, particularly to a critical audience.

I want to review these three kinds of situations in which risk analysis can be applied.

I have mentioned that detailed fault trees are most useful when risk analysis is used as an integral part of the design process. In this first application the probabilities are relatively unimportant, although they do have some role in optimizing the design. The main object of the fault tree is to identify which are the significant failure modes. As soon as a failure mode is found to be significant, evaluation stops and a design change is made. Risk-assessment methods are of enormous value, precisely because, in this application, there need not be a heavy reliance on the subjective probabilities.

I suspect that the design applications of risk analysis are of great importance to this Commission, and I look forward to hearing more on this subject from the other speakers. But I will leave this area behind, except for one truism that bears repeating.

I've sometimes had the experience of riding as a passenger on nuclear submarines, and observing the interaction among their officers and crew as they operate their on-board nuclear power plants. Submariners are a dedicated breed, and a good portion of their lives is given over to playing "what if" games concerning potential emergencies and irregularities. They ask questions such as, "What if that valve were to stick open, or that circuit breaker were to trip? What caused it, what will happen next, and what am I going to do about it?"

What they are really doing is constructing informal fault trees. It is part of their training, to improve their emergency responses. The truism is that some of the most important components of any system are the human components, and that design of the human components—that is, training—doesn't stop with installation of the hardware. Risk analysis should continue in support of that training. The probabilities are not critical to this application either; but a direct link between the analyst and the crew or its training program is essential.

The second class of applications for risk analysis is in support of a single decision maker, who is able to participate directly in the analysis process itself.

This is an ideal situation for risk analysis, because there is a basis on which to assign the subjective probabilities: that is, the judgment of the client, the single decision maker. I do not mean to imply that the client is always right, or that the analyst should not attempt to influence the client's opinions. But ultimately, the client is going to make his decisions within the context of his own subjective judgments; and he will find the analyst's calculations useful only if they are consistent with those judgments.

The situation of a single decision maker is so advantageous, from the point of view of finding a rational way to cope with risk, that it is worth going to substantial pains to bring actual cases within this framework. In particular, it is desirable to seek institutional arrangements of the sort that bring parties together to study a problem from the same point of view, rather than making risk analyses into tools for advancing competing interests.

According to the working paper, this Commission's major concern is with risk to lives of crew members on offshore drilling units. In this case the interested parties might include: the companies that build. and operate the platforms; the workers, with their unions and representatives; and government agencies charged with insuring worker safety. The parties' interests differ, but they share a common interest in accurate information, and it might optimistically be hoped that they will be able to agree on common assumptions for a risk assessment. They are more likely to reach such a consensus if their interests are made as nearly as possible to coincide; for example, by a sound system of compensation and insurance.

The analyst faces a much more challenging task in the third class of applications, when his analysis is to be used as evidence in a complex, multi-party decision process. In this case, the intended audience may include many different parties with widely differing interests and different assumptions.

There is now no proper basis for the required subjective inputs. Consequently, the analyst has no clearly acceptable means of producing an exact, quantitative conclusion consistent with the often-conflicting assumptions of the parties involved. If he uses subjective inputs provided by his own client, he will quite rightly seem biased in the eyes of other parties.

In this situation the role of the analyst is, first, to provide a logical framework for the interaction of the parties. He may also be able to provide objective values for some of the required inputs to his calculations, and perhaps a range of acceptable values on others. Ultimately he may be able to provide upper and lower bounds for the final estimates which are acceptable to all parties.

The Commission would be dealing with this third class of applications, if the risk of environmental damage from offshore drilling were to become a major political issue in Canada.

I want to close by proposing a list of questions that we should ask concerning any intended application of risk analysis.

(4) Who is the intended audience for the results? And finally,

Answering these questions at the outset will help us to get the best from the variety of available techniques.

[a] Decisions with Multiple Objectives: Preferences and Value Tradeoffs, by Ralph L. Keeney and Howard Raiffa, John Wiley & Sons, New York, 1976.

[b] Risk Analysis and Decision Processes by Howard C. Kunreuther and Joanne Linnerooth, John Lathrop, Hermann Atz, Sally Macgill, Christoph Mandl, Michiel Schwarz, and Michael Thompson, Springer-Verlag, New York, 1983.

[c] The Risk Analysis Controversy: An Institutional Perspective Howard C. Kunreuther and Eryl V. Ley, Editors, Springer-Verlag, New York, 1982.

[d] "Principles of Unified Systems Safety Analysis," by B. John Garrick, Nuclear Engineering and Design, Vol. 13, 1970, pp. 245-321.

[e] Siting Energy Facilities, by R. L. Keeney, Academic Press, New York, 1980.

[f] "Science and Trans-science," by A. M. Weinberg, Minerva, Vol. 10, 1972, pp. 209-222 (Quoted in reference [g]).

[g] "Low Probability Accidents," by Kunreuther and Linnerooth, Risk Analysis, to appear.

Walter R. Stromquist
132 Bodine Road, Berwyn, PA 19312
walters-at-chesco.com